Ch6: Continuous Random Variables
- For continous random variables we generally have
- For continous variables we need another kind of model, where we find probabilities for x being in an interval. this is a probability density function or pdf
probability density function
non-negative function f, such that
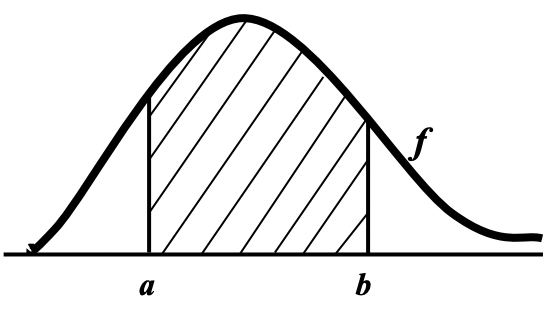
- In this definition probabilities are areas: the probability that x takes the values between a and b is equal to the area below the graph.
- Open or Close interval does not affect the probability.
Properties
If a function has these two conditions then it is a pdf
Distribution Function
Distribution Function
The function F defined by
Properties
For any distribution function:
- F is non decreasing.
- if
- if
- F is continuous from the right
Properties
INFO
A random variable X is continuous if the distribution function F of X is a continous function.
Properties of Continous distributions
closed interval equals open interval - If the density function f(x) of X is symetric about x = c, then E(X) = c.